'Profiles' of protein structures and sequence alignments can detect subtle homologies. Profile analysis has been put on firmer mathematical ground by the introduction of hidden Markov model (HMM) methods. During the past year, applications of these powerful new HMM-based profiles have begun to appear in the fields of protein-structure prediction and large-scale genome-sequence analysis.

Computational analysis is increasingly important for inferring the functions and structures of proteins [1] because the speed of DNA sequencing has long since surpassed the rate at which the biological function of sequences can be elucidated experimentally. Established sequence comparison algorithms detect significant similarities between known database sequences and 35-80% of new proteins, depending on the organism. Increasing this percentage is of the utmost importance. An increase of a single percentage point may mean learning something useful about an additional 700 human proteins by the time elucidation of the sequence of the human genome nears completion round about the year 2002.

Pairwise sequence comparison methods such as BLAST and FASTA generally assume that all amino acid positions are equally important even though a great deal of position-specific information is usually available for a protein or protein family of interest. Multiple alignments of protein sequence families indicate residues that are more conserved than others, and the points at which insertions and deletions are more frequent. Three-dimensional (3D) structural information allows structural environments to be taken into account when scoring aligned residues, and allows insertions and deletions to be expected more frequently in surface loops than in core secondary structure elements. A 'profile' (defined as a consensus primary structure model consisting of position-specific residue scores and insertion or deletion penalties) is an intuitive step beyond the pairwise sequence alignment methods. Profile methods based either on multiple sequence alignments [2] [3] [4] or on 3D structures [5] [6] have been independently developed by a number of groups, and are widely used.

The problem with profiles is that they are complicated models with many free parameters. One is faced with a number of difficult problems: what are the best ways to set the position-specific residue scores, to score gaps and insertions, and to combine structural and multiple sequence information? Until recently, these questions have generally been addressed in an ad hoc fashion. An ad hoc scoring system can be expertly tuned by trial and error to be adequate, but a consistent mathematical basis is still desired.

New profile methods using 'hidden Markov models' (HMMs) have been introduced to address the above questions. In this review, I will explain what HMMs are, describe their strengths and limitations, and highlight how HMM-based profiles are beginning to be used in protein structure prediction and large-scale genome sequence analysis.

Hidden Markov models

David Haussler, Anders Krogh and their colleagues at University of California, Santa Cruz recognized that all the profile methods could be expressed as HMMs. Their lucid technical report was widely circulated, and the work ultimately appeared in the open literature in early 1994 [7]. By this time, other groups were already exploring HMM-based profile methods [8] [9].

Hidden Markov models are a general statistical modeling technique for 'linear' problems like sequences or time series and have been widely used in speech recognition applications for twenty years. HMMs had been used before in computational sequence analysis [10], including applications to protein structural modeling [11] [12]. Haussler's work was aimed so clearly at the popular profile analysis methods that it elevated HMMs into the consciousness of a wider community. Within the HMM formalism, it is possible to apply formal, fully probabilistic methods to profiles and gapped sequence alignments.

What is an HMM?

The key idea is that an HMM is a finite model that describes a probability distribution over an infinite number of possible sequences.

A wonderfully clear description of HMM theory has been written by Rabiner [13]. One speaks of an HMM 'generating' a sequence. The HMM is composed of a number of states, which might correspond to positions in a 3D structure or columns of a multiple alignment. Each state 'emits' symbols (residues) according to symbol-emission probabilities, and the states are interconnected by state-transition probabilities. Starting from some initial state, a sequence of states is generated by moving from state to state according to the state-transition probabilities until an end state is reached. Each state then emits symbols according to that state's emission probability distribution, creating an observable sequence of symbols. Fig. 1 shows a simple HMM for a heterogeneous DNA sequence [10].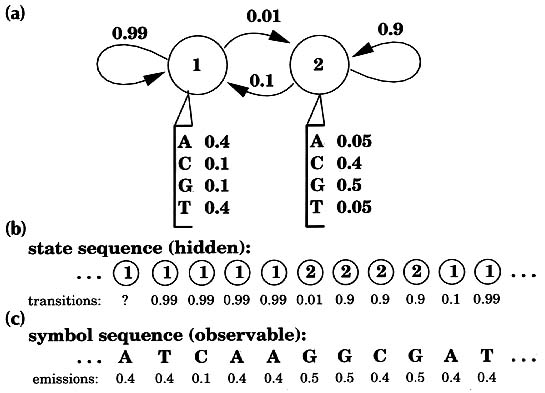

Figure 1 A simple hidden Markov model. A two-state HMM describing DNA sequence with a heterogeneous base composition is shown, following work by Churchill [10]. (a) State 1 (top left) generates AT-rich sequence, and state 2 (top right) generates CG-rich sequence. State transitions and their associated probabilities are indicated by arrows, and symbol emission probabilities for A,C,G and T for each state are indicated below the states. (For clarity, the begin and end states and associated state transitions necessary to model sequences of finite length have been omitted.) (b) This model generates a state sequence as a Markov chain and each state generates a symbol according to its own emission probability distribution (c). The probability of the sequence is the product of the state transitions and the symbol emissions. For a given observed DNA sequence, we are interested in inferring the hidden state sequence that 'generated' it, that is, whether this position is in a CG-rich segment or an AT-rich segment.

Why are they called hidden Markov models? The sequence of states is a Markov chain, because the choice of the next state to occupy is dependent on the identity of the current state. However, this state sequence is not observed: it is hidden. Only the symbol sequence that these hidden states generate is observed. The most likely state sequence must be inferred from an alignment of the HMM to the observed sequence.

In general, when using HMMs we are interested in solving one of three problems [13]. First, given an existing HMM and an observed sequence, we want to know the probability that the HMM could generate the sequence (the scoring problem). Second, we want to know the optimal state sequence that the HMM would use to generate the sequence (the alignment problem). Third, given a large amount of data, we want to find the structure and parameters of the HMM which best account for the data (the training problem). Haussler and his colleagues' insight was that profiles can be rewritten as HMMs, and that these problems are exactly analogous to the problems of scoring sequences with profiles, finding optimal sequence-profile alignments, and constructing profiles from unaligned as well as aligned protein or DNA sequence data.

HMM-based profiles

An example of an HMM-based profile is shown in Fig. 2. Most of the columns of a multiple sequence alignment are assigned to 'match' states. Each of the match states has an emission distribution that reflects the probability of seeing a given residue in that position. Each match state is also accompanied by two other states. A 'delete' state emits nothing, allowing a column to be skipped, which is a deletion relative to the consensus. An 'insert' state exists between each pair of match states and it has a state transition to itself. This allows one or more symbols to be inserted at any point relative to the consensus.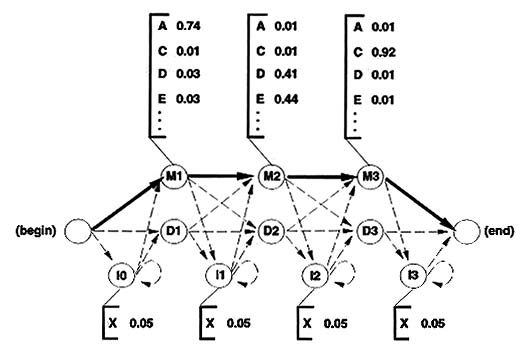

Figure 2 An HMM-based profile. An example of an HMM-based profile of three positions is shown, following the model introduced by Krogh et al. [7oo]. Each important column of a multiple sequence alignment (top) is modeled by a triplet of states: match (M), insert (I), and delete (D). For each modeled column of the alignment, there are 49 parameters: nine state transition probabilities (arrows), 20 match state symbol emission probabilities (corresponding to the bracketed amino acid residues [single letter code]), and 20 insert state symbol emission probabilities (usually not learned from the alignment, but instead kept fixed at some background distribution). For the sake of clarity in this example, all the insert symbol emissions are shown set equally to 0.05, underlining the point that the inserts generate essentially 'random' residue sequence. The state transition probabilities will generally tend to favor a 'main line' through the match states (bold arrows) over the rarer paths containing insertions and deletions (dashed arrows).

The HMM formalism makes two major contributions. First, HMMs can be trained from unaligned as well as aligned data, whereas standard profiles require a pre-existing multiple alignment. Second, HMM-based profiles use a justifiable statistical treatment of insertions and deletions. In standard profiles, it is impossible to determine optimal insertion/deletion scores except by trial and error, and the statistical significance of an alignment has to be evaluated by empirical methods. Since handling insertions and deletions is a major problem in recognizing highly divergent protein sequences, the recasting of profiles as HMMs promises a significant increase in the power of profiles to recognize distantly related structural homologs.

Assumptions of HMMs and profiles

HMM-based profiles make two important assumptions. First, pairwise (or higher order) correlations between residues are ignored. An HMM is a primary structure model. That is not to say that HMMs are necessarily just sequence models: the 3D structural environment of a position can be taken into account. For instance, 3D profiles, in which the residue scores are determined by a position's structural environment and have nothing to do with sequence [5], can be usefully implemented as HMMs. Similarly, many of the protein 'inverse folding' methods that use a so-called 'frozen approximation' [14] (so that dynamic programming algorithms can be used for alignment and scoring) can be expressed usefully as HMM methods. Second, HMMs assume that sequences are generated independently from the model. Real biosequences are related by common evolutionary descent and are highly non-independent. This is probably the major outstanding problem with any profile method. My colleagues and I [9] have described alternatives to maximum likelihood HMM training methods that compensate for the biased sequence sampling caused by evolutionary trees, but these methods are indirect and essentially amount to new HMM-style sequence-weighting methods. Mitchison and Durbin [15] explored a tour de force fusion of maximum likelihood phylogeny reconstruction with hidden Markov models, but the algorithms used are not yet computationally practical.

HMM-based multiple sequence alignment

Unlike profiles, HMMs can be trained from a set of unaligned example sequences, producing a multiple alignment in the process. The speech recognition field provides a well-studied training algorithm called the Baum-Welch algorithm, which Krogh et al. [7oo] employed. Baldi et al. [8] [16] have described the use of an alternative HMM training algorithm using gradient descent which seems equally effective. Both approaches find locally optimal alignments, not globally optimal ones, and they occasionally get stuck in incorrect optima. Krogh et al. [7] used a 'noise injection' heuristic to avoid local optima. I have described a simulated annealing variant of Krogh's approach which is even less prone to local optima [17]. This and related work has shown that HMM methods can be used to sample suboptimal sequence alignments according to their probability [18] [19].

HMM-based multiple alignment is interestingly different from most previous multiple alignment methods. The scoring parameters as well as the alignment are initially unknown. Alignment, therefore, does not require difficult a priori choices for scoring parameters. Also, the HMM approach avoids the computationally intractable many-to-many multiple sequence alignment problem by recasting it as a tractable many-to-one sequence-HMM alignment problem. Indeed, aligning sequences to a common consensus model is intuitively much closer to what we want a multiple alignment to represent in the first place. Current HMM methods are approaching the accuracy of existing approaches, and will often outperform other multiple alignment algorithms in complicated cases involving many gaps and insertions [17].

HMM-based protein homolog recognition

Krogh et al showed that the first HMM-based profiles were slightly superior to standard profiles for protein homolog recognition [7]. Tim Hubbard and his colleagues applied HMM methods in combination with secondary-structure prediction tools in a protein structure prediction competition in 1994. Hubbard's predictions were about as accurate as the predictions made by the much more complicated threading algorithms for protein inverse folding [19]. Hubbard's HMMs were exclusively based on sequence alignments. Because HMMs are well suited for smoothly combining sequence and structural environment information, further HMM-based incursions into the inverse folding and threading fields may be expected.

A drawback of the first HMM-based profile methods was that they required a large number of sequences (> 100) for good homolog recognition. Significant advances have now been made in incorporating prior information about amino acid substitution probabilities into HMMs, using either 'mixture Dirichlet' priors [20] [21] or Dayhoff PAM (per cent accepted mutation) substitution matrices [22]. Effective HMMs for homolog recognition can now be constructed from a handful of sequences.

Pairwise similarity search algorithms (BLAST and FASTA) are effective on relatively disorganized databases. In contrast, because HMMs are based on aligned sequence families instead of single sequences, the application of HMM-based profiles to large-scale genome or database analysis requires hierarchical second generation databases of protein families and sequence alignments. In collaboration with the producers of the hierarchically organized SCOP (structural classification of proteins) database [23], Erik Sonnhammer has produced a database of domain sequence alignments and hidden Markov models (E Sonnhammer, SR Eddy, unpublished data). This alignment database currently models 100 different protein domain families and is available on the World Wide Web (http://www.sanger.ac.uk/Pfam). HMM-based analysis of protein domains and DNA repeat families is beginning to supplement BLAST analysis of nematode, yeast, and human DNA sequencing efforts at the genome centers at Washington University in St. Louis, USA, and the Sanger Centre in Cambridge, UK.

Conclusions

Hidden Markov model based profiles have resolved many of the problems associated with standard profile analysis. HMMs provide a consistent theory for scoring insertions and deletions, and a consistent framework for combining structural and sequence information. HMM-based multiple sequence alignment is rapidly improving. HMM-based homolog recognition is already sufficiently powerful for HMM methods to compare favorably to much more complicated threading methods for protein inverse folding. Software for HMM-based profiles that will run on almost any UNIX platform is freely available from http://www.cse.ucsc.edu/research/compbio/sam.html or from http://genome.wustl.edu/eddy/hmmer.html.

It is important to bear in mind that HMM-based profiles are a very special case of HMM approaches. HMM methods are being pressed into use for a variety of biological problems, such as gene prediction [24], protein secondary structure prediction [25], and even the construction of radiation hybrid maps [26].

The philosophy we adopt in using HMMs is that complicated structure-sequence analysis problems are best addressed as statistical inference problems using full probabilistic models. An increasingly active field of research is the development of other full probabilistic approaches for problems more complicated than HMMs can handle, such as RNA secondary structure analysis using stochastic context-free grammars [27] [28] or dealing with pairwise correlation in protein sequences (i.e. threading methods and their kin) using Markov random fields [29] [30]. It is useful to think about these and other full probabilistic models in the framework of the Chomsky hierarchy of formal grammars, introduced by Chomsky for problems in computational linguistics [31]. Searls [32] has written an excellent introduction to the use of linguistic approaches in biosequence analysis.

In just two years, HMM-based profiles have moved from pure theory to practical application in protein-structure prediction and large-scale genome sequence analysis. Bits of HMM theory, such as the use of mixture Dirichlet priors, are being mainstreamed into other analysis methods [33]. As a devout partisan of HMMs and full probabilistic approaches, I think that the usefulness and range of HMM applications in structural biology can only continue to grow.

Acknowledgements

I thank my colleagues in the Cambridge (UK) computational biology discussion group, particularly Graeme Mitchison and Richard Durbin, for a deluge of ideas. My work on HMMs has been graciously supported by postdoctoral fellowships from the Human Frontier Science Program (LT-130/92) and the National Institutes of Health (1-F32-GM16932), and is currently supported by Washington University.

References and recommended reading

1. Altschul SF , Boguski MS , Gish W , Wooton JC :
Issues in searching molecular sequence databases.
Nat Genet 1994, 6: 119Ð129.

2. Barton GJ :
Protein multiple sequence alignment and flexible pattern matching.
Methods Enzymol 1990, 183: 403Ð427.

3. Gribskov M , McLachlan AD , Eisenberg D :
Profile analysis: detection of distantly related proteins.
Proc Natl Acad Sci USA 1987, 84: 4355Ð4358.

4. Taylor WR :
Identification of protein sequence homology by consensus template alignment.
J Mol Biol 1986, 188: 233Ð258.

5. Bowie JU , Luthy R , Eisenberg D :
A method to identify protein sequences that fold into a known three-dimensional structure.
Science 1991, 253: 164Ð170.

6. Luthy R , Bowie JU , Eisenberg D :
Assessment of protein models with three-dimensional profiles.
Nature 1992, 356: 83Ð85.

7. Krogh A , Brown B , Mian IS , Sjolander K , Haussler D :
Hidden Markov models in computational biology: applications to protein modeling.
J Mol Biol 1994, 235: 1501Ð1531.
This is the paper that introduced the use of HMM methods for protein and DNA sequence profiles.

8. Baldi P , Chauvin Y , Hunkapiller T , McClure MA :
Hidden Markov models of biological primary sequence information.
Proc Natl Acad Sci USA 1994, 91: 1059Ð1063.

9. Eddy SR , Mitchison G , Durbin R :
Maximum discrimination hidden Markov models of sequence consensus.
J Comput Biol 1995, 2: 9Ð23.
This paper constitutes a principled HMM-style contribution to the ever-increasing number of sequence-weighting methods. It introduces an alternative to maximum likelihood parameter estimation that compensates for biased sequence representation.

10. Churchill GA :
Stochastic models for heterogeneous DNA sequences.
Bull Math Biol 1989, 51: 79Ð94.

11. Stultz CM , White JV , Smith TF :
Structural analysis based on state-space modeling.
Protein Sci 1993, 2: 305Ð314.

12. White JV , Stultz CM , Smith TF :
Protein classification by stochastic modeling and optimal filtering of amino-acid sequences.
Math Biosci 1994, 119: 35Ð75.

13. Rabiner LR :
A tutorial on hidden Markov models and selected applications in speech recognition.
Proc IEEE 1989, 77: 257Ð286.

14. Godzik A , Kolinski A , Skolnick J :
Topology fingerprint approach to the inverse protein folding problem.
J Mol Biol 1992, 227: 227Ð238.

15. Mitchison GJ , Durbin RM :
Tree-based maximal likelihood likelihood substitution matrices and hidden Markov models.
J Mol Evol 1995, 41: 1139Ð1151.

16. Baldi P , Chauvin Y :
Smooth on-line learning algorithms for hidden Markov models.
Neural Computation 1994, 6: 305Ð316.

17. Eddy SR :
Multiple alignment using hidden Markov models.
In Proceedings of the Third International Conference on Intelligent Systems for Molecular Biology. Edited by Rawlings C, Clark D, Altman R, Hunter L, Lengauer T, Wodak S. Menlo Park: AAAI Press, 1995, 114Ð120.

18. Allison L , Wallace CS :
The posterior probability distribution of alignments and its application to parameter estimation of evolutionary trees and to optimization of multiple alignments.
J Mol Evol 1994, 39: 418Ð430.
The authors' work is HMM-ish in character, but written in the language of information theory (minimum message length) rather than probabilistic modeling (maximum likelihood). The contrast is instructive.

19. Shortle D :
Protein fold recognition.
Nat Struct Biol 1995, 2: 91Ð93.
This is a short review of the Asilomar conference, at which current methods for protein structure prediction were rigorously compared. Be aware, though, that Shortle confuses threading methods, which deal with pairwise residue correlations in protein structure, with HMMs, which don't.

20. Brown M , Hughey R , Krogh A , Mian IS , Sjolander K , Haussler D :
Using Dirichlet mixture priors to derive hidden Markov models for protein families.
Proceedings of the First International Conference on Intelligent Systems for Molecular Biology. Edited by Hunter L, Searls D, Shavlik J. Menlo Park. AAAI Press, 1993, 47Ð55.

21. Karplus K :
Evaluating regularizers for estimating distributions of amino acids.
Proceedings of the Third International Conference on Intelligent Systems in Molecular Biology Edited by Rawlings C, Clark D, Altman R, Hunter L, Lengauer T, Wodak S. Menlo Park. AAAI Press, 1995, 188Ð196.

22. Baldi P :
Substitution matrices and hidden Markov models.
J Comput Biol 1995, 2: 487Ð491.

23. Murzin A , Brenner SE , Hubbard T , Chothia C :
SCOP: a structural classification of proteins database for the investigation of sequences and structures.
J Mol Biol 1995, 247: 536Ð540.

24. Krogh A , Mian IS , Haussler D :
A hidden Markov model that finds genes in E. coli DNA.
Nucleic Acids Res 1994, 22: 4768Ð4778.
This is a nice illustration of the power of HMM methods to integrate various kinds of information into a single probabilistic model. Krogh's gene model includes a statistical description of ribosome binding sites, start and stop codons, codon usage, and intergenic repetitive elements.

25. Asai K , Hayamizu S , Handa KI :
Prediction of protein secondary structure by the hidden Markov model.
Comput Appl Biosci 1993, 9: 141Ð146.

26. Lange K , Boehnke M , Cox DR , Lunetta KI :
Statistical methods for polyploid radiation hybrid mapping.
Genome Res 1995, 5: 136Ð150.

27. Eddy SR , Durbin R :
RNA sequence analysis using covariance models.
Nucleic Acids Res 1994, 22: 2079Ð2088.

28. Haussler D , Sakakibara Y , Brown M :
Stochastic context-free grammars for tRNA modeling.
Nucleic Acids Res 1994, 22: 5112Ð5120.

29. Berger B , Wilson DB , Wolf E , Tonchev T , Milla M , Kim PS :
Predicting coiled coils by use of pairwise residue correlations.
Proc Natl Acad Sci USA 1995, 92: 8259Ð8263.
The importance of taking pairwise residue correlations into account in protein sequenceÐstructure analysis is controversial. If pairwise correlation is relatively unimportant, HMMs can be as good as the more complicated 'threading' methods for protein inverse folding for a fraction of the computational cost. To date, this paper is one of the few arguments for the importance of modeling pairwise residue correlations that I find convincing. The approach of Berger et al is a simple Markov random field, although they don't explicitly call it such in the paper.

30. White JV , Muchnik I , Smith TF :
Modeling protein cores with Markov random fields.
Math Biosci 1994, 124: 149Ð179.

31. Chomsky N :
Three models for the description of language.
IRE Transactions in Information Theory 1956, 2:

32. Searls DB :
The linguistics of DNA.
Am Sci 1992, 80: 579Ð591.

33. Tatusov RL , Altschul SF , Koonin EV :
Detection of conserved segments in proteins: Iterative scanning of sequence databases with alignment blocks.
Proc Natl Acad Sci USA 1994, 91: 12091Ð12095.

Author Contacts
Sean R Eddy, Department of Genetics, Washington University School of Medicine, 660 South Euclid, Box 8232, St. Louis, MO 63110, USA; e-mail: eddy@genetics.wustl.edu

Latest update of content: May 20, 2003

Ralf Koebnik
Institut de recherche pour le dèveloppement
UMR 5096, CNRS-UP-IRD
911, Avenue Agropolis, BP 64501
34394 Montpellier, Cedex 5
FRANCE
Phone: +33 (0)4 67 41 62 28
Fax: +33 (0)4 67 41 61 81
Email: koebnik(at)gmx.de
Please replace (at) by @.