Hidden Markov models are a general statistical modeling technique for 'linear' problems like sequences or time series and have been widely used in speech recognition applications for twenty years.
What is an HMM? The key idea is that an HMM is a finite model that describes a probability distribution over an infinite number of possible sequences.
HMM-based profiles The HMM formalism makes two major contributions. First, HMMs can be trained from unaligned as well as aligned data, whereas standard profiles require a pre-existing multiple alignment. Second, HMM-based profiles use a justifiable statistical treatment of insertions and deletions. In standard profiles, it is impossible to determine optimal insertion/deletion scores except by trial and error, and the statistical significance of an alignment has to be evaluated by empirical methods.
Assumptions of HMMs and profiles HMM-based profiles make two important assumptions. First, pairwise (or higher order) correlations between residues are ignored. Second, HMMs assume that sequences are generated independently from the model. HMM-based multiple sequence alignment HMMs can be trained from a set of unaligned example sequences, producing a multiple alignment in the process. There are two approaches which are used to calculate the parameters of the model (symbol-emission probabilities and state-transition probabilities). Both find locally optimal alignments, not globally optimal ones, and they occasionally get stuck in incorrect optima. Already in 1996, HMM methods were approaching the accuracy of existing approaches, and were predicted to outperform other multiple alignment algorithms in complicated cases involving many gaps and insertions. Modified from: Sean Eddy (1996)
An HMM is a graph of connected states, each state potentially able to "emit" a series of observations.
Profile HMMs Anders Krogh and colleagues have developed a hidden Markov model equivalent of profile analysis for investigating protein families (Krogh et al., 1994). Profile analysis provided an ad hoc way to represent the "consensus profile" of amino acids for a set of protein sequences belonging to the same family. The hidden Markov model applied was deliberately modeled on this successful technique, but introduced the notion of using probability-based parameterization, allowing both a principled way of setting the gap penalty scores and also more novel techniques such as expectation maximization to learn parameters from unaligned data. 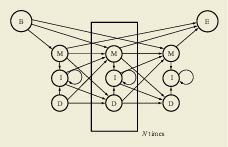
A profile HMM, which has a repetitive structure of three states (M, I, and D). Each set of three states represents a single column in the alignment of protein sequences. The architecture of the HMM is shown in Figure 1. It has a simple left-to-right structure in which there is a repetitive set of three states, designated as match, delete, and insert (M, D, and I). The match state represents a consensus amino acid for this position in the protein family. The delete state is a non-emitting state, and represents skipping this consensus position in the multiple alignment. Finally, the insert state models the insertion of any number of residues after this consensus position. The success of HMMER (Eddy, 2001), an enhanced profile HMM software package, in providing a stable, robust way to analyze protein families gave rise to a number of databases of hidden Markov models. Such databases are similar in many ways to the databases of phonemes and longer words used in speech recognition: Since biology has a limited number of protein families in existence, sheer enumeration of these protein domains is achievable. Despite the early promise of using unsupervised training approaches to derive these HMMs, highly supervised approaches by bioinformatics experts have always outperformed the more automatic approaches. The databases of profile HMMs are therefore focused around manual adjustment of the profile HMMs followed by an automatic gathering of complete datasets from large protein sets, as illustrated by the use of the Pfam (protein family database) (Bateman et al., 2002) and SMART (simple modular architecture research tool) (Letunic et al., 2002) approaches. Pfam in particular now possesses coverage significant enough that 67% of proteins contain at least one Pfam profile HMM and 45% of residues in the protein database are covered in total by the HMMs. This extent of coverage, coupled with the good statistical behavior of the profile HMMs, has made Pfam an automatic protein classification system without peer. Modified from: E. Birney (2001)
Profile hidden Markov models (profile HMMs) are statistical models of the primary structure consensus of a sequence family. Anders Krogh, David Haussler, and co-workers at UC Santa Cruz introduced profile HMMs (Krogh et al., 1994), adopting HMM techniques which have been used for years in speech recognition. HMMs had been used in biology before the Krogh/Haussler work, but the Krogh paper had a particularly dramatic impact, because HMM technology was so well-suited to the popular "profile" methods for searching databases using multiple sequence alignments instead of single query sequences. Since then, several computational biology groups (including ours) have rapidly adopted HMMs as the underlying formalism for sequence profile analysis. "Profiles" were introduced by Gribskov and colleagues (Gribskov et al., 1987; Gribskov et al., 1990) at about the same time that other groups introduced similar approaches, such as "flexible patterns" (Barton, 1990), and "templates" (Bashford et al., 1987; Taylor, 1986). The term "profile" has stuck.1 All of these are more or less statistical descriptions of the consensus of a multiple sequence alignment. They use position-specific scores for amino acids (or nucleotides) and position specific scores for opening and extending an insertion or deletion. Traditional pairwise alignment (for example, BLAST (Altschul et al., 1990), FASTA (Pearson and Lipman, 1988), or the Smith/Waterman algorithm (Smith and Waterman, 1981)) uses position-independent scoring parameters. This property of profiles captures important information about the degree of conservation at various positions in the multiple alignment, and the varying degree to which gaps and insertions are permitted. The advantage of using HMMs is that HMMs have a formal probabilistic basis. We can use Bayesian probability theory to guide how all the probability (scoring) parameters should be set. Though this might sound like a purely academic issue, this probabilistic basis lets us do things that the more heuristic methods cannot do easily. For example, an HMM can be trained from unaligned sequences, if a trusted alignment isn't yet known. Another consequence is that HMMs have a consistent theory behind gap and insertion scores.2 In most details, HMMs are a slight improvement over a carefully constructed profile - but far less skill and manual intervention is necessary to train a good HMM and use it. This allows us to make libraries of hundreds of profile HMMs and apply them on a very large scale to whole-genome or EST sequence analysis. One such database of protein domain models is Pfam (Sonnhammer et al., 1997); the construction and use of Pfam is tightly tied to the HMMER software package. HMMs do have important limitations. One is that HMMs do not capture any higher-order correlations. An HMM assumes that the identity of a particular position is independent of the identity of all other positions.3 HMMs make poor models of RNAs, for instance, because an HMM cannot describe base pairs. Also, compare protein "threading" methods, which include scoring terms for nearby amino acids in a three-dimensional protein structure. A general definition of HMMs and an excellent tutorial introduction to their use has been written by Rabiner (Rabiner, 1989). For a review of profile HMMs, see (Eddy, 1996), and for a complete book on the subject of probabilistic modeling in computational biology, see (Durbin et al., 1998). 1 There has been some agitation to call all such models "position specific scoring matrices", PSSMs, but certain small nocturnal North American marsupials have a prior claim on the mnemonic.
From: Sean Eddy (2001)
Latest update of content: September 26, 2005 Ralf Koebnik
| ||||||||||||||||||||||||
